Tutorial (Part 1): Implementing the GJK Distance Algorithm with EPA in 3D space

Intro

About the tutorial

Welcome! I am glad you found your way to this tutorial.

First part

In the first part of this tutorial, we go through the basics of the GJK (Gilbert–Johnson–Keerthi) distance algorithm and focus only on determining whether two convex bodies in 3D space are intersecting.

Second part

In the second part, we will focus on the EPA (Expanding Polytope Algorithm) extension and how to compute the distance, penetration depth, and separating vector.

Additional future parts

At the time of writing, I am planning to write at least the first two parts of this tutorial.

Author

I am Severi Suominen, experienced software engineer, start-up founder, C++ enthuastic equipped with a burning passion for game engines, gameplay, 3d, graphics programming and optimization.

You can visit the about page or my portfolio to get to know me better.

Motivation

Learning to work with 3D geometry and related techniques can be intimidating and overwhelming, especially without an academic background. As concepts become more advanced, learning materials tend to be sparse and often difficult to follow.

I believe that making these topics more accessible to video game developers—and software developers in general—through easy-to-follow tutorials will not only equip them with new tools but also introduce new ways of thinking and problem-solving.

Objectives

1. Write an efficient, educational implementation of the GJK distance algorithm with the EPA extension.
2. Learn about the use cases, limitations, and potential improvements of the algorithms.
3. [Optional] To have fun and insightful time learning!

Prerequisities

1. Familiarity with C++17 (basics of the language features, templates, containers and memory management).
2. Familiarity with the concept of indexed meshes.
3. A basic understanding of linear algebra is required (but I will walk you through some concepts related to this implementation).
4. A math library of your choice that includes vector and matrix types (glm, raymath). You can also use mxlib, a simplistic single header C++17 math/utility library I wrote specifically to use with my tutorials. Otherwise we will be relying only on the standard library.
5. [Optional] Environment/library for 3D visualizations (Raylib is a great option)

Caution

The implementation written in this tutorial is educational and intended to demonstrate the basics of the GJK distance algorithm, not to provide a solid, out-of-the-box, production-ready solution. At least for the first two parts of the tutorial, to keep it simple, we will be omitting the more advanced features and techniques, we also won’t address issues with numerical instability. These could be a great topics for the future parts of the tutorial.

In the tutorial we will be using 32-bit floating point numbers, so there is not much precision to work with, and every calculation is merely an approximation (as always with floating point number types). This causes number instability issues and edge cases, especially with parametric shapes or more complicated models. Less distinct features naturally lead to more issues with precision, which accumulate over iterations. The GJK distance algorithm implementation works best when used with polyhedra and even a simpler version of the algorithm is very solid for these shapes.

The real challenge of implementing this algorithm is making it solid while supporting a large variety of shapes (even concave geometry with decomposition algorithm) while maintaining efficiency. This is not a trivial task, but I encourage you to explore various techniques to achieve this—or perhaps we can even explore them together in future parts of this tutorial.

Demo

Demo including the implementation and visualizations can be found from s2cpp-monorepo, demo can be easily build with CMake.

Pre-built binaries available for Windows

Demo including the algorithm implementation is licensed under MIT license.

So what are GJK and EPA?

To avoid unnecessary repetation I might refer to Gilbert–Johnson–Keerthi distance algorithm simply as GJK and the Expanding Polytope Algorithm as EPA

Gilbert–Johnson–Keerthi distance algorithm

The GJK (Gilbert–Johnson–Keerthi) distance algorithm is a method for finding the shortest distance between two convex bodies in 2D, 3D, or any arbitrary-dimensional space. Due to its efficiency, the algorithm is widely used for collision detection in video games and real-time physics simulations. It is also sometimes employed in graphics rendering for more accurate culling of complex objects.

The basic idea is to compute the Minkowski difference (also known as erosion) between two convex bodies and check whether it contains the origin or find the distance from the origin to the closest geometric primitive (point, edge, surface…). However, since bodies can contain a large number of points, computing all possible differences between them quickly becomes exponentially demanding. This makes real-time applications impractical if relying on a brute-force approach with a more complex geometry.

Luckily GJK offers an efficient and creative solution to this problem. Instead of computing all possible points of the Minkowski difference, it iteratively constructs a simplex to search the Minkowski difference. It does this utilizing a support function to find the furthest pair of points of the bodies in a given direction and then calculate the Minkowski difference for that specific pair.

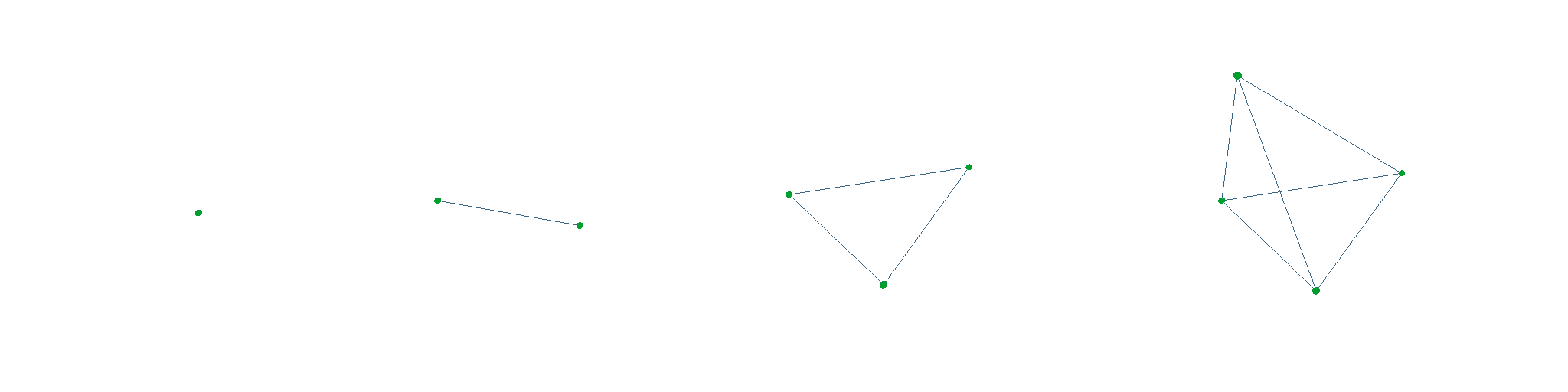
A simplex is the simplest possible polytope in any given dimension. In 3D space, the possible simplex shapes are:

• Point (0D)
• Line segment (1D)
• Triangle (2D)
• Tetrahedron (3D)

Simplex in 0D, 1D, 2D and 3D.

During each iteration, the simplex is updated based on a series of plane distance tests to determine its relationship to the origin.

The algorithm refines the simplex step by step, moving it closer to the origin with each iteration, finally resulting to a simplex that is as close as possible, or containing the origin.

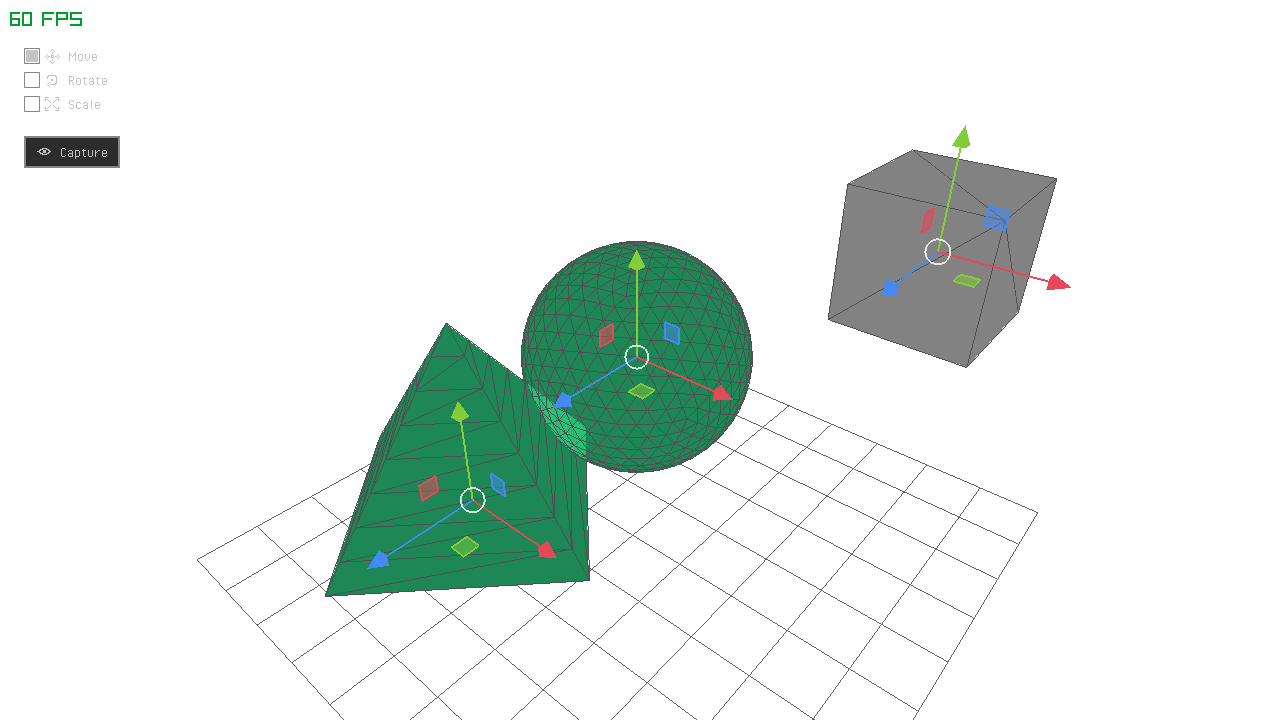
If at any point, the simplex (which forms a tetrahedron in 3D) encloses the origin, it confirms that an intersection has occurred. The image on the right is demonstraiting the refinement process over iterations.

What makes GJK special?:

• Extremely efficient, providing a near-constant time complexity solution for a problem that has generally been solved in quadratic time complexity (Separating Axis Theorem).

Limitations of GJK algorithm:

• Works only with convex bodies (decomposition algorithm required for concave shapes)
• Only provides information if an intersection is happening, without providing us the penetration depth or separating vector used to consruct the MTV (Minimum Translation Vector) for resolving penetration. This is where the EPA extension comes in handy.
• Number instability, especially problematic with parametric shapes, requires finding balance between performance and accuracy (for example deciding between 32 bit or 64 bit floating point number precission, or even using more expensive integer arithmetic)

Expanding polytope algorithm

EPA (Expanding Polytope Algorithm) is used as an extension of the GJK algorithm to determine the penetration depth and separating vector of overlapping bodies. This is done by taking the tetrahedral simplex obtained from the GJK algorithm and expanding it into a polytope by adding new support points until a stable edge is found. The identified edge provides the penetration depth and separating vector (how much and in which direction the convex body needs to be pushed to resolve the penetration).

We will get into the details of EPA further in the next part of this tutorial.

What makes EPA special?:

• Provides a solution to find the penetration depth and separating vector, helping to overcome one of the biggest limitations of the GJK distance algorithm.
• Extremely efficient, usually takes only a few iterations to find a suitable edge.

Limitations of EPA algorithm:

• Works only with convex bodies, same as with GJK distance algorithm.
• General complexity, there are many edge cases that need to be handled correctly.
• Even more number instability, numerical instability can cause issues with accuracy and affect performance if not handled correctly.

Minkowski sum and difference

Minkowski difference of sphere and cube visualized

Minkowski sum and difference might sound intimidating, but in reality there’s nothing too complicated about them. To calculate Minkowski sum of two set of points, we could write something like:

std::vector<xfloat3> minkowski_sum{};

for(int i = 0; i < a_points.size(); i++) {
    for(int j = 0; j < b_points.size(); j++) {
        // we add every point in A to every point of B
        const auto sum = b_points[j] + a_points[i];
        minkowski_sum.push_back(sum);
    }
}

Looking at the code we can see that its really nothing but a quadratic operation where we sum all possible pairs of points between the sets A and B.

To calculate Minkowski difference of two set of points, we don’t need to change much:

std::vector<xfloat3> minkowski_diff{};

for(int i = 0; i < a_points.size(); i++) {
    for(int j = 0; j < b_points.size(); j++) {
        // we just subtract instead
        const auto difference = b_points[j] - a_points[i];
        minkowski_diff.push_back(difference);
    }
}

Minkowski sum and difference are not actually considered as a distinct concepts, but a variants of the same thing. Reason for this is that a difference can be interpreted as a sum with the inverse, and vice versa. So fundamentally we are talking about the same thing:

// sum
const auto sum = b_points[j] + a_points[i];

// still sum
const auto difference = b_points[j] + (-a_points[i]);

For this implementation we are only interested in Minkowski difference, as it has a very useful feature demonstrated in the image below.

Minkowski difference of sphere and cube in different positions

Looking at the image, we can observe a very interesting phenomenon. Whenever the two bodies are overlapping, regardless of where the overlap occurs in the world, the Minkowski difference (calculated for both objects in the above image) always contains the white dot at the zero coordinates, representing the origin of the space.

All we need to do is encapsulate the origin inside the Minkowski difference to confirm that an intersection of the bodies is occurring.

And this is exactly what we are going to do next!

Implementation

So now that we have at least some level of understanding of what GJK and EPA are about, we can begin the implementation. If you still feel unsure, no need to worry—we will approach the implementation step by step while gradually becoming more familiar with the concepts.

1. Define data structures and utility

Math types like struct xfloat4x4 or struct xfloat3 as well as the class fixed_list<T, N> container type, are from my mxlib math/utility library, but any other 3D/linear algebra library works too, and std::vector can be used as a substitute for the class fixed_list

Lets start from the more simple things and define some data structures.

Mesh object

First we will define struct mesh_object that represents a convex body

struct mesh_object
{
    // local-to-world matrix for transforming vertices to a common world space, you can use
    // compose function in your math library to create a model matrix from 
    // position, rotation and scale
    xfloat4x4
    _model_mtx{};

    // pointer to vertex array (if you are storing vertices in std::vector,
    // you can obtain the pointer with .data() function)
    xfloat3*   
    _vertices{};

    // count of vertices
    uint32_t
    _vertex_count{};
};

Support point

Next we will define struct support_point that represents a point in Minkowski difference

struct support_point 
{
    // stored for EPA
    xfloat3 _support_a{};

    // stored for EPA
    xfloat3 _support_b{};

    // position in Minkowski difference
    xfloat3 
    _position{};
};

[Optional] By-Products Data for Visualization

Then, we will define an optional struct by_products_data whose sole purpose is to store any data needed for visualizing the algorithm. For the first part of the tutorial, it will store the simplex positions for drawing.

struct by_products_data
{   
    // using std::vector or similar is fine
    fixed_list<xfloat3, 4> 
    _simplex_points{};
};

[Optional] Math helper functions

in case you are not familiar with the concepts of dot product or cross product, I recommend you to check out this crash course Mastering the concepts of dot and cross product in 10 minutes

Finally, we might want to define generic mixed_product() and triple_product() math utility functions (that usually are not implemented in most math libraries) to keep our code neat and tidy. As can be seen from the code these are mainly shorthand functions for specific vector multiplication operations:

mixed_product

dot_product(cross_product(v0, v1), v2)

triple_product

cross_product(cross_product(v0, v1), v2)

// mxlib.hpp

template<typename T>
T mixed_product(const xvec3<T>& v0, const xvec3<T>& v1, const xvec3<T>& v2) {
    return dot_product<T>(cross_product<T>(v0, v1), v2);
}

template<typename T>
xvec3<T> triple_product(const xvec3<T>& v0, const xvec3<T>& v1, const xvec3<T>& v2) {
    return cross_product<T>(cross_product<T>(v0, v1), v2);
}

or in case you do not want to use templated functions:

float mixed_product(const xvec3<float>& v0, const xvec3<float>& v1, const xvec3<float>& v2) {
    return dot_product(cross_product(v0, v1), v2);
}

xvec3<float> triple_product(const xvec3<float>& v0, const xvec3<float>& v1, const xvec3<float>& v2) {
    return cross_product(cross_product(v0, v1), v2);
}

2. GJK function and validation

As a starting point for the GJK implementation, we declare an intersects() function under the gjk() namespace. This function will be used to test whether two convex bodies are colliding.

Instead of returning a simple boolean value indicating whether an intersection has occurred, we define an 8-bit-wide bitmask enum result_bits to encode and return additional information. This bitmask will store a flag indicating if an intersection has occurred, along with useful validation data for debugging. This approach efficiently utilizes available resources, especially since boolean values are almost always padded to at least 8 bits (or 1 byte).

#include <cstdint>
...
namespace gjk
{
   typedef enum result_bits : uint8_t {
        // empty mask
        GJK_EMPTY_MASK                    = 0,    // 0000 0000
        // validation bits
        GJK_INVALID_BIT                   = 0x1,  // 0000 0001
        GJK_ERROR_SAME_OBJECT_BIT         = 0x2,  // 0000 0010
        GJK_ERROR_NULL_OBJECT_BIT         = 0x4,  // 0000 0100
        GJK_ERROR_SAME_VERTEX_ARRAY_BIT   = 0x8,  // 0000 1000
        GJK_ERROR_NULL_VERTEX_ARRAY_BIT   = 0x10, // 0001 0000
        GJK_ERROR_NOT_ENOUGH_VERTICES_BIT = 0x20, // 0010 0000
        // result bits
        GJK_INTERSECTING_BIT              = 0x40, // 0100 0000
        // lets leave the last bit 
        // for later use cases
        GJK_EXTRA_BIT                     = 0x80, // 1000 0000
    } result_bits;

    static result_bits intersects (
        // pointers to convex bodies
        const mesh_object* alpha_, 
        const mesh_object* beta_, 
        // max iterations we allow until we force exit
        uint32_t max_iter_ = 1000, 
        // pointer to optional by-products object to store information for 
        // visualization/debug purposes, can be null
        by_products_data* by_products = nullptr);
...

After declaring the intersects() function and defining the enum result_bits bitmask type, we will implement the function in the source file (or at the end of the .hpp file if you prefer a header-only approach).

#include "cg_gjk.hpp"
// math functions
#include "mxlib.hpp"
...
using namespace gjk;
using namespace mxlib;

uint8_t gjk::intersects (
    const mesh_object* alpha_, 
    const mesh_object* beta_, 
    uint32_t max_iter_, 
    by_products_data* by_products);
{

// implementation...

The first thing we want to add to the function is a validation check to ensure that the argument values are suitable for our GJK implementation. Specifically, we want to confirm that:

• Objects A and B are not pointing to a same object in memory
• Objects are not pointing to a null memory
• Vertex arrays are not pointing to a same array sequence and position in memory
• Vertex arrays are not pointing to a null memory
• Both vertex arrays contains enough vertices to form a 3D volumetric shape

In this tutorial we won’t test convexity of bodies as this would add a lot of overhead relative to GJK distance algorithm implementation (potentially many times more expensive), and assuming static geometry is used this should be tested only once on import anyway, instead of every time we do a intersection test. If you are interested there are many ways to test convexity of 3D bodies:

• Half-space testing with hyperplanes
• Convex hull algorithms (QuickHull)
• Minkowski sum
• Testing dihedral angles

Performing these checks and encoding the information into a bitmask could look something like this:

// argument validation checks
uint8_t validation_error_bits = 
    !(alpha_ != beta_) << 1 |
    !(alpha_ && beta_) << 2;
    
if(validation_error_bits == GJK_EMPTY_MASK)
{
    // A and B object pointers can be dereferenced, add rest of the checks
    validation_error_bits |=
    !(alpha_->_vertices != beta_->_vertices)  << 3 |
    !(alpha_->_vertices && beta_ ->_vertices) << 4 |
    !(alpha_->_vertex_count >= 3 && beta_ ->_vertex_count >= 3) << 5;
} 

The basic idea can be explained as follows:

0 << num_bits_to_shift will always evaluate to 0, while 1 << num_bits_to_shift will always evaluate to 2 ^ num_bits_to_shift. In other words, it produces a single or zero bit value where num_bits_to_shift acts as a zero-based position index.

We can improve the above code to enhance readability. Let’s define a macro.

// we could define macro:

#define MASK_IF_FALSE(cond,mask) (!(cond))*(mask)

// but using functions should always be preferred instead of macros
// whenever possible for better code readability and minimizing error proneness. 
// Debugging complicated macros in a large code base can be a real pain.

// with C++17 we could create something like this,
// in most cases generated instructions are equivalent with the macro version.
template<auto MASK>
inline constexpr auto mask_if_false(const bool cond) {
    return !cond * MASK;
}

...

// note: since C++11 we can get the underlying number type of enum at compile time
// to make code less vulnerable for changes:
std::underlying_type<gjk::result_bits>::type validation_error_bits = 
    mask_if_false<GJK_ERROR_SAME_OBJECT_BIT>(alpha_ != beta_) |
    mask_if_false<GJK_ERROR_NULL_OBJECT_BIT>(alpha_ && beta_);

if(validation_error_bits == GJK_EMPTY_MASK) {
    // A and B object pointers can be dereferenced, add rest of the checks
    validation_error_bits |= 
    mask_if_false<GJK_ERROR_SAME_VERTEX_ARRAY_BIT>(
        alpha_->_vertices != beta_->_vertices) |
    mask_if_false<GJK_ERROR_NULL_VERTEX_ARRAY_BIT>(
        alpha_->_vertices && beta_ ->_vertices) |
    mask_if_false<GJK_ERROR_NOT_ENOUGH_VERTICES_BIT>(
        alpha_->_vertex_count >= 3 && beta_->_vertex_count >= 3);
}

In the above code, I created a helper function to multiply an enum value (representing a bit) by the evaluated (inverted) condition.

Finally, we check whether validation_error_bits contains any bits. If it doesn’t, this indicates that validation was successful. However, if any bits are present at this stage, we add a bit to the bitmask to indicate a validation failure and exit the function, returning the bitmask with the error bits.

if(validation_error_bits  != GJK_EMPTY_MASK) {
    // add the invalid bit '0000 0001' as validation was not successful
    validation_error_bits |= GJK_INVALID_BIT;
    return static_cast<gjk::result_bits>(validation_error_bits);
}

As an example the usage of this function could look something like this:

const auto result_bits = gjk::intersects(body_a, body_b, 100, nullptr);

if(mxlib::contains(result_bits, gjk::GJK_INTERSECTING_BIT))
{
    // <insert here some very cool out of this world video game physics>
} 
else 
{
    if(mxlib::contains(result_bits, gjk::GJK_INVALID_BIT))
    {
        if(mxlib::contains(result_bits, gjk::GJK_ERROR_NULL_OBJECT_BIT)){
            printf("Intersect called with a nullptr object argument\n");
        }

        if(mxlib::contains(result_bits, gjk::GJK_ERROR_SAME_OBJECT_BIT)){
            printf("Intersect called with object arguments pointing to a same object\n");
        }
        ...
    }
}

// or we could have a test case asserting:
TEST_CASE_ASSERT (
    !mxlib::contains(result_bits, gjk::GJK_INVALID_BIT | gjk::GJK_INTERSECTING_BIT),
    "Invalid intersect results should never be marked as intersecting");

Common pitfall: (bitmask1 & bitmask2) != 0 works well for checking whether a bitmask is contained within another bitmask as long as the right, left, or both operands contain exactly one or zero bits. However, if you are working with bitmasks that may have multiple bits set or if you are unsure about the bit count, always use (bitmask1 & bitmask2) == bitmask2.

3. Transforming vertices

Next, we will add a new helper function, transform_mesh_object_vertices_to_ws() to a source file. This function takes a struct mesh_object* as an argument and returns a std::vector populated with vertex positions transformed from model space to world space (local-to-world). To achieve this, we will multiply the vertex positions by the object’s model matrix.

static std::vector<xfloat3> transform_mesh_object_vertices_to_ws(
    const gjk::mesh_object* mesh_object_)
{   
    const auto& model_mtx    = mesh_object_->_model_mtx;
    const auto  vertex_count = mesh_object_->_vertex_count;

    auto ws_vertices = std::vector<xfloat3>();
    // pre-allocate memory since we know the size of vertices,  
    // allowing us to allocate memory only once.
    ws_vertices.resize(vertex_count);

    for(int i = 0; i < vertex_count; ++i) {
        // transform the vertex from local space to world space  
        // by multiplying it with the model matrix.
        ws_vertices[i] = mxlib::transform(mesh_object_->_vertices[i], model_mtx);
    }

    // RVO (Return Value Optimization): No extra copies are made when returning  
    // a function-scope object like this.
    return ws_vertices;
};

Then, all that’s left to do is call this function for both convex bodies and retrieve the world space vertices. We will transform the vertices only once, at the beginning of the gjk::intersects() function, after the validation checks.

<validation code>
...
// transform vertices to world space
auto wverts_a = transform_mesh_object_vertices_to_ws(alpha_);
auto wverts_b = transform_mesh_object_vertices_to_ws(beta_);

4. Support function

Support function is the cornerstone of this algorithm used to construct the search simplex. the function will take a arbitary direction search_direction and vertex array pointers and vertex counts of both bodies verts_a verts_b count_a count_b as an arguments.

The basic idea is straight-forward

1. First we find the best matching position for each sets of vertices in a given direction.
2. Then we calculate Minkowski difference by subracting the pair of positions.

Lets split the support function into two separate parts to avoid unnecessary code duplication.

static xfloat3 find_support_point (
    const xfloat3& search_direction, 
    const xfloat3* verts,
    const uint32_t count)

static support_point find_minkowski_support (
    const xfloat3& search_direction, 
    const xfloat3* verts_a, 
    const xfloat3* verts_b,
    const uint32_t count_a,
    const uint32_t count_b);

First we implement the find_support_point() function responsible of finding the best matching vertex position (the furthest vertex in a search direction), we will calculate dot products of the vertices and the given direction, the largest product being the best match.

There are many ways to skin the cat when it comes to traversing geometry. Since we do not consider vertex indices in this implementation (nor any vertex attributes in addition to position), we implicitly support both convex hulls of point clouds and indexed meshes, and we want to keep it that way. Furthermore, as data pre-processing is beyond the scope of this tutorial, and acceleration structures or sorting would just add overhead without any benefits unless vertex counts are very large, we will stick to simply iterating through the vertex arrays one-by-one in a straightforward yet cache-friendly manner.

// find_support_point 

if(count == 0) { return {0,0,0}; }

// finding a vertex with the highest product with a search direction,
// this is easily tested by calculating and comparing dot products of a search direction 
// and vertex positions.
auto best_index = 0;
auto best_match = dot_product(search_direction, verts[0]);
for(int i = 1; i < count; ++i){
    const auto dot = dot_product(search_direction, verts[i]);
    if(dot > best_match) {
        best_index = i;
        best_match   = dot;
    }
}

return verts[best_index];

Then we implement the find_minkowski_support() function responsible of calculating the Minkowski difference of the best matching vertex positions.

// find_minkowski_support 

support_point point = {};

// find the best matching vertex positions, stored to be later used with EPA.
// Note that we use a negated (multipling vector with -1) search direction 
// for finding the support point A.
point._support_a = find_support_point(negate(search_direction), verts_a, count_a);
point._support_b = find_support_point(search_direction, verts_b, count_b);

// calculate Minkowski Sum (difference in our case) by subtracting A and B support positions,
point._position = point._support_b - point._support_a;

return point;

5. Initialization

Now that we have implemented our support function, we will return to the gjk::intersects() function and use it to find the initial support point for initializing a simplex.

First, we need to decide which direction to use as the initial search direction.

The initial search direction can be any arbitrary vector—it does not affect the correctness of the algorithm but can impact performance. Estimating a search direction that aligns well with the origin is generally better than using a constant direction vector.

// gjk::intersects

...

// - OPTION 1: 
// an arbiraty constant direction

// AABB min to max normalized diagonal vector  
auto search_direction = xfloat3{0.577f, 0.577f, 0.577f};

// - OPTION 2: 
// Use the non-normalized direction from object A to object B,  
// this is a commonly used and fairly accurate estimate.  

// we obtain the translation (or world position)  
// from the last column of the object's model matrix.  

// note: This example assumes a column-major order matrix.  
// If your matrix is stored in row-major order,  
// use indices 12, 13, and 14 instead.  
const auto wpos_a = xfloat3(alpha_->_model_mtx[3], alpha_->_model_mtx[7], alpha_->_model_mtx[11]);
const auto wpos_b = xfloat3(beta_->_model_mtx[3], beta_->_model_mtx[7], beta_->_model_mtx[11]);

// we can calculate direction from object A to object B by subtracting
auto search_direction = wpos_b - wpos_a;

After choosing our search direction we can find the initial support point and create the simplex object.

// gjk::intersects

...

// finding a support point best matching the chosen search direction
const auto initial_support_point = 
    find_minkowski_support(
        search_direction,
        wverts_a.data(), 
        wverts_b.data(), 
        wverts_a.size(), 
        wverts_b.size());

// using std::vector instead of fixed_list as the simplex type is fine. 
fixed_list<support_point, 4> simplex{};

simplex.add(initial_support_point);

// set up the next search direction used to promote the simplex to a line segment,  
// note that the next search direction should always be oriented towards origin,
// we can use negation to flip the direction of the initial support point position
//  to achieve this.
search_direction = negate(initial_support_point._position); 

6. Simplex testing and refining

Almost there! So now that we have:

1. Defined all data structures and helper functions
2. Validated the function arguments
3. Transformed all vertices to world space
4. Implemented the support function
5. Created and initialized the simplex
6. Set the next search direction

We are finally ready to face the final boss of this algorithm implementation. Testing and refining the simplex is the most complicated part of the implementation, but the basic iteration logic is straight-forward.

First we create loop to iteratively test and modify the simplex. In beginning of each iteration, we find a new support point based on the current search direction and add it to the simplex, then perform tests to find out if the simplex is containing the origin, and if necessary, modifying the simplex based on the current simplex configuration and its relation with the origin.

// gjk::intersects

...

uint32_t iter = 0;

while(1) 
{
    // finding the next support point
    auto support_point = 
        find_minkowski_support(
            search_direction,
            wverts_a.data(), 
            wverts_b.data(), 
            wverts_a.size(), 
            wverts_b.size());

    // if we are beyond the origin we know there is no overlap, we can early exit
    if(dot_product(support_point._position, search_direction) < 0) {
        // intersection not happening, we will return GJK_EMPTY value
        return GJK_EMPTY_MASK;
    }
    
    // add a new support point to the simplex
    simplex.add(support_point);

    if(test_simplex(simplex, search_direction)) {
        // simplex is tetrahedron containing the origin,
        // intersection is happening
        break;
    }
        
    ++iter;

    if(iter > max_iter_){
        // if 'iter' reaches 'max_iter_' we assume we have fallen into infinite loop 
        // scenario caused by a number instability and the objects are 
        // in a very close proximity of each other (or intersecting), in this 
        // tutorial we aim for a simple implementation meant to be educational,
        // we will assume intersection is happening in this case.  
        break;
    }
}

// intersection is happening between objects, we will return GJK_INTERSECTING_BIT
return GJK_INTERSECTING_BIT;

Lets create the simplex testing and refining function test_simplex()

static bool test_simplex(fixed_list<support_point, 4>& simplex, xfloat3& direction)

This is the function where the real magic of this implementation happens. We perform series of plane distance tests relative to the current set of support points, guided by these tests we know how to modify the simplex to find a combination of support points that forms a tetrahedron containing the origin.

There are many ways to implement these tests and the approach we are using in this tutorial is more or less the same as with the Casey Muratori’s technique. Getting these tests right is crucial for the correctness and performance of the algorithm.

Some visualization of the simplex refinement rules in action, the red point clouds are representing points in the Minkowski difference of the object pairs.

Simplex refinement rules

We will skip the 0D case as there is not much to test with only single point, so we begin from the 1D case. With these rules we are heavily utilizing dot product, cross product, mixed product and triple product, you can visit this section if you need to refresh your memory.

If you find it hard to follow or intuitively understand this part of the tutorial, visualization is your best friend!

Hyperplanes and point-plane distance.

To determine how we need to refine the simplex based on the lines and surfaces formed by the support points, we use vectors representing the surface normals of infinite planes that split the 3D space into two half-spaces—these are known as hyperplanes. The concept of a hyperplane consists of two components: a scalar and a vector, which represent the plane’s distance from the origin and its surface normal, respectively. The fundamental formula for calculating a hyperplane is:

plane_normal   =  normalize(input_direction);
plane_distance = -dot_product(plane_normal, input_position);

and to find the shortest distance from a point to a planar surface:

dot_product(plane_normal, point) + plane_distance;

In our case, since the translation of the planes is always zero, we can omit the plane distance value entirely. This allows us to simplify the equation, reducing it to a single dot product calculation.

dot_product(plane_normal, point);

In addition to that, we only need to consider the sign of the dot product. In other words, we only need to determine whether a point lies in front of or behind the plane.

Case 1D - Line

The line simplex case is straightforward. As with all these cases, the details and explanations are embedded in the code for clarity.

// test_simplex

// case 1D - line
if(simplex.size() == 2)
{
    // direction of the line, from 0 to 1
    xfloat3 d01 = simplex[1]._position - simplex[0]._position;

    // direction towards the origin: 
    // since the vertex position (or its translation from the origin) 
    // always points away from the origin, we can simply negate it 
    // to obtain the reversed direction toward the origin.
    xfloat3 dto = negate(simplex[0]._position);

    // is the line pointing towards the origin?
    if(dot_product(d01, dto) > 0) {

        // perpendicular explained:
        // two geometric objects are perpendicular when they intersect at exactly a 90-degree angle (or π/2 radians).
        // a useful characteristic to remember is that the dot product of two perpendicular vectors is always zero.
        //
        //           line1
        //             |   
        //    line0 ___|___
        //
        // looking at the crude visualization above, we can say 
        // line0 and line1 are perpendicular.

        // we calculate perpendicular of the line (towards the origin) to use 
        // as the next search direction to find suitable support point
        // to form a triangle 
        xfloat3 perp_01 = triple_product(d01, dto, d01);
        direction = perp_01;
    } else {
        // line was not pointing towards the origin, so we will use the negated position(A) 
        // of the simplex as the next search direction, we can be certain its pointing
        // towards the origin
        direction = dto;
    }

    return false;
}

Case 2D - Triangle

The triangle simplex case is the most complicated because there are multiple directions to expand, depending on the simplex’s relationship to the origin.

// test_simplex

...

// case 2D - triangle
if(simplex.size() == 3)
{
    // 1 _____ 0
    //   \   /
    //    \ /              
    //     2

    // triangle forming lines 2 => 0 and 2 => 1,
    
    // we call these lines "right" and "left"  
    // to make this part easier to conceptualize. 
   
    // "right" line
    xfloat3 d20 = simplex[0]._position - simplex[2]._position;
    // "left" line
    xfloat3 d21 = simplex[1]._position - simplex[2]._position;

    // direction towards the origin
    xfloat3 dto = negate(simplex[2]._position);

    // we calculate perpendicular (or normal) of the triangle surface by calculating
    // the cross product of the triangle forming lines.   
    xfloat3 perp = cross_product(d21, d20); 
        
    // is the origin on the "right" side of the triangle?
    if(mixed_product(perp, d20, dto) > 0) {
        // is the "right" line facing the origin? 
        if(dot_product(d20, dto) > 0) {
            // set the next search direction towards the origin.
            direction = triple_product(d20, dto, d20);
            // remove the point that is not part of the "right" line.
            simplex.remove(1);
            return false; 
        }
    } 
    // is the origin on the right side of the "left" line? 
    else if(mixed_product(d21, perp, dto) <= 0) {
        if(dot_product(perp, dto) > 0) {
            // the origin is above 
            direction = perp;
        } else {   
            // the origin is below,
            //
            // swap points 0 and 1 to maintain
            // the correct order of the triangle,
            // or in other words, to ensure the
            // surface normal remains correctly oriented.
            simplex.swap(0, 1);
            direction = negate(perp);
        }
        return false;
    }

    // is the "left" line facing the origin?
    if(dot_product(d21, dto) > 0){
        // set the next search direction towards the origin.
        direction  = triple_product(d21, dto, d21);
        // remove the point that is not part of the "left" line.
        simplex.remove(0);
    } 
    else {
        // if we reach this point, we can't refine the simplex
        // in any meaningful way based on the current set of points.
        // We will reset the simplex, set the next search direction to DTO,
        // and start over.
        direction = dto;
        simplex.reset();
    }

    return false;
}

Case 3D - Tetrahedron

In the tetrahedral simplex case, only three tests remain to determine if the formed tetrahedron contains the origin.

For each newly formed triangle and its direction toward the origin, we calculate the plane’s distance to determine whether the origin is contained within the hyperplane of the surface.

// test_simplex

...

// case 3D - tetrahedron
if(simplex.size() == 4)
{
    //       3
    //      /|\
    //     / | \
    //    /  |  \
    //   1'-.|.-'0
    //       2

    // tetrahedron forming lines 3 => 2, 3 => 1, 3 => 0
    xfloat3 d32 = simplex[2]._position - simplex[3]._position;
    xfloat3 d31 = simplex[1]._position - simplex[3]._position;
    xfloat3 d30 = simplex[0]._position - simplex[3]._position;
    
    // direction towards the origin
    xfloat3 dto = negate(simplex[3]._position);

    // perpendicular vector for the each newly formed triangle surface,
    // notice the clockwise order.
    xfloat3 perp321 = cross_product(d32, d31);
    xfloat3 perp310 = cross_product(d31, d30);
    xfloat3 perp302 = cross_product(d30, d32);

    // there are only three tests left  
    // to determine if the formed tetrahedron contains  
    // the origin.  
      
    // for each newly formed triangular surface and  
    // the direction towards the origin, we calculate  
    // the plane distance to determine whether the  
    // origin is contained within the surface's  
    // hyperplane.  
      
    // if the origin is not contained within the triangle's plane,  
    // we know it lies in front of the triangle.  
    // In this case, we remove the only support point  
    // that is not part of the triangle from the simplex,  
    // set the next search direction to the normal  
    // of the triangle surface, and then exit to form a new tetrahedron.  
     
    // if the origin is contained within all the triangle planes,  
    // we return 'true' from this function, indicating that  
    // the origin is enclosed within the simplex.

    if(dot_product(perp321, dto) > 0) {
        direction = perp321;
        simplex.remove(0);
    }
    else if(dot_product(perp310, dto) > 0) {
        direction = perp310;
        simplex.remove(2);
    }
    else if(dot_product(perp302, dto) > 0) {
        direction = perp302;
        simplex.remove(1);
    }
    else {
        // we have encapsulated the origin! 
        return true;
    }
}

With the above set of rules we can refine a simplex towards the origin in a very efficient way.

And we are done!

Congratulations! You have now implemented a simple, bare-bones version of the GJK distance algorithm (without the actual distance part yet, currently only testing for overlaps).

We still don’t know the distance, penetration depth or the separation direction. We will explore how we can compute these values in the next part of the tutorial.

The current implementation will tell us if two convex bodies in 3D space are intersecting, at least when numerical instability is not causing issues with more challenging geometries or with very close proximity operations in general.

Finalizing the implementation

In case you want to visualize the algorithm and didn’t do it already, you can add the final simplex points (and additional information) to the by-produts data object.

Outro

The final words

I hope you enjoyed the first part of the tutorial.

Any feedback is more than welcome, especially if you found something confusing, misleading, or incorrect. The integrity and correctness of these tutorials is important to me, so your help is greatly appreciated.

Leave a comment!