Crash course: Mastering the concepts of dot and cross product in 10 minutes

About the tutorial

As dot product and cross product are vector multiplication operations fundamental to working with 3D, I decided to make this brief post to summarize these concepts in a simple and on-the-point manner, making it easier for readers not familiar, or looking to find a more intuive ways to think these concepts, to follow the other tutorial posts.

Objectives

1. To understand the key aspects of the dot product and cross product.

Demo

You can get the demo from s2cpp-monorepo. The demo can be easily build with CMake and contains some scripts for a quick setup, demo is licensed under MIT license, excluding media assets with a separate license file present.

Pre-built binaries available for Windows

Dot product

The dot product is simply the component-wise sum of the vector obtained by multiplying two vectors element-wise. For example if we have 3 dimensional vectors: v0 and v1, the dot product of these vectors is:

float dot_product = v0.x*v1.x + v0.x*v1.x + v0.x*v1.x; 

The dot product is useful to measure how much one vector goes in the direction of another.

Properties

• If the value is positive, the vectors are facing the same direction.
• If the value is negative, the vectors are facing opposite directions.
• If the value is zero, the vectors are perpendicular (at 90 degrees or π/2 radians) to each other.
• The dot product has a direct relationship with the cosine of the angle between the vectors.

Example use cases

• Calculating the angle between two vectors.
• Aligning a vector with a given direction.
• Dividing space into positive and negative half-spaces, such as finding a point’s distance from a plane.
• Determining how much force is applied in a certain direction in physics simulations.
• Keeping character movement aligned with a surface in video games.
• Checking if a camera is looking at an object.
• Rendering shadows and reflections in 3D graphics.

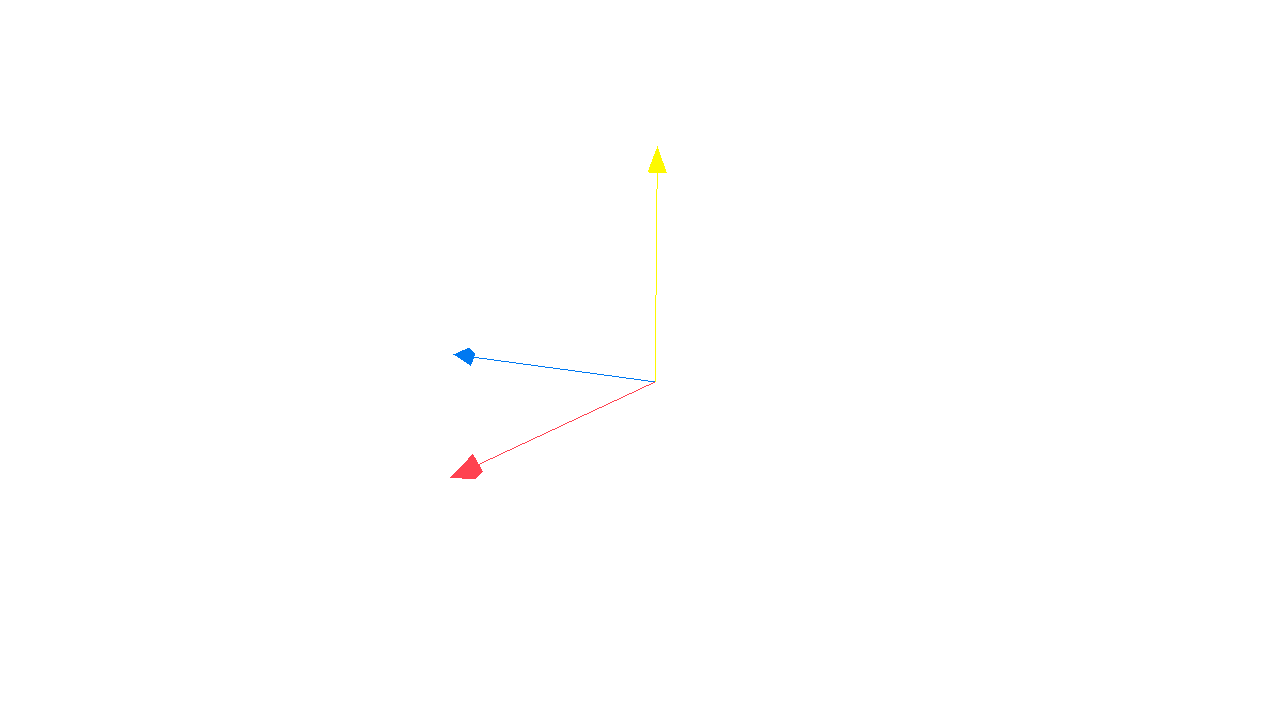
Cross product

The cross product is a bit more complicated and result in vector instead of scalar. For vectors v0 and v1, the cross product is:

float3 cross_product = {
    v0.y*v1.z - v0.z*v1.y,
    v0.z*v1.x - v0.x*v1.z,
    v0.x*v1.y - v0.y*v1.x,
};

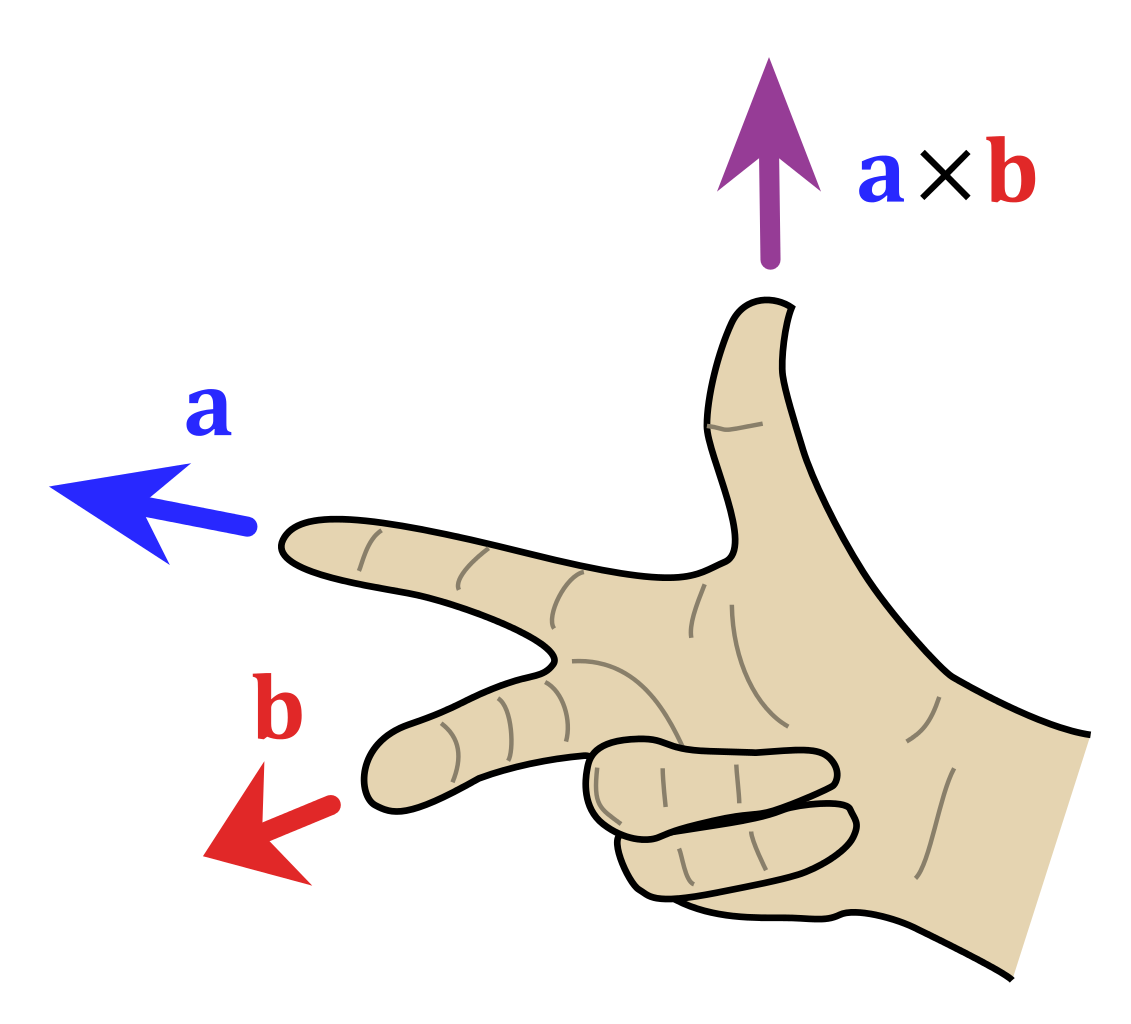
Right hand rule

The direction of the resulting vector follows the right-hand rule.

If we look at the image on the right, “A” being the first argument vector and “B” being the second argument vector.

If you point your right-hand fingers along the “A” vector and curl them toward the “B” vector, your thumb points in the direction of the cross product.

Properties

• Not Commutative! The order of the operands matter.
• The result of the cross product is always a vector, not a scalar.
• The resulting vector is perpendicular to both input vectors.
• If the two vectors are parallel or anti-parallel, the result is zero vector.
• The magnitude of the cross product is proportional to the sine of the angle between the two vectors:

Example use cases

• Finding a vector perpendicular to two given vectors.
• Calculating surface normals for lighting and shading in 3D graphics.
• Computing angular velocity in physics simulation.
• Ensuring objects maintain correct orientation and rotation in 3D space.